Benchmarks

Here we compare performance of Redberry with the similar software. At the moment there are a lot of packages and CASs which provide functionality for symbolic tensor manipulation. As far as we know, the architecture of existing open source systems is based on the principal of indices canonicalization — an algorithm which brings indices of tensorial expressions to unique canonical order thereby providing a simple way for expression comparison, while Redberry uses another approach (see Notes on internal architecture). For our purposes we choose Cadabra (version 1.29) which is based on the xPerm library for tensor canonicalization and Mathematica package xAct version 1.1.0 (uses the recent xPerm version). Recently, Maple (starting from Maple 18 Physics research version 42.1 released in December 2014) also implemented functionality for simplifying tensorial expressions which were previously unavailable (e.g. most of the examples provided below failed in previous Maple Physics versions). Since Maple and its Physics package are proprietary, the underlying architecture is not known.

In the performance evaluation we focused specifically on manipulation with abstract tensorial expressions avoiding special cases for which different systems can be additionally optimized (like manipulation with Riemann tensor). In order to analyse performance of systems for particular class of problems we proceed as follows. We used a set of randomly generated tensors with different parameters (number of free indices, depth, average product/sum size, set of basic tensors from which the expression was composed). Each initial expression was simplified by expanding out products of sums and reducing similar terms, then rewritten in the equivalent form by: (1) shuffling product/sum terms, (2) renaming dummies and (3) interchanging indices of simple tensors according to their symmetries. Each benchmark was performed on expression obtained by subtracting rewritten expression from the initial one. We measured time needed for different systems to obtain zero by applying simplification operation on such input. Such simplification frequently occurs in real computations and involves many internal components of CAS.

We used the following simplification procedures:

• In case of Redberry we used the following transformation to obtain zero:

  def tr = EliminateMetrics & 'd^i_i = 4'.t &
           Expand[EliminateMetrics & 'd^i_i = 4'.t] &
           EliminateMetrics & 'd^i_i = 4'.t &
           EliminateDueSymmetries
  

• The following code was used in Cadabra (Cadabra spacetime dimension set to 4):

  @sumflatten!!(%):@prodflatten!!(%):
  @eliminate_metric!(%):@eliminate_kr!(%):
  @distribute!(%):@sumflatten!!(%):@prodflatten!!(%):
  @eliminate_metric!(%):@eliminate_kr!(%):
  @prodsort!(%):@canonicalise!(%):@prodsort!(%):
  @rename_dummies!(%):@prodsort!(%):@collect_terms!(%);
  

  We tried a variety of combinations of Cadabra transformations and found that this one works faster and covers largest number of cases. When a single invocation of this code did not produce zero (this occurred in less than 1% of cases), we applied it several times (but not more then ten). We analysed each of such cases in more detail and found that they can be solved by changing the above sequence of Cadabra transformations in one run.

• In case of xAct we used function ToCanonical[] which performs almost the same steps as described above.

• Maple defines no special transformations for operations with tensors like collect similar terms or eliminate metric. It provides only one transformation Simplify, which is used for any simplification of tensorial expressions (we've specifically contacted Maple Physics developers and they suggested using Simplify with tryhard option which enables Simplify to work with tensors; they also assured us that this option will be default in the future Maple releases). When a single invocation of Simplify did not produce zero, we applied it twice (increase of the number of retries does not change the number of correct results). In case of non-zero result, test was considered as failed; such cases are excluded from consideration.

The expressions used for performance benchmarking can be found below. The source code used for expressions generation and benchmark execution is available on request.

In our first benchmark we measured performance of comparison operation, which is probably the most frequent atomic operation arising in any calculation. For this purpose, we generated sums of products of tensors and measured time needed to obtain zero when subtracting it (rewritten in equivalent form as described earlier) from itself.

As we have found, the existing systems fails on some expressions with complicated structure. For example, if tensor $W_{abcde}$ is fully symmetric in indices $a,c,e$ then the following expression is zero: \begin{multline*} T^{h} \, (W_{bde}{}^{ij}+W_{bde}{}^{ji}+W_{bed}{}^{ij}+W_{dbe}{}^{ji}+W_{de}{}^{i}{}_{b}{}^{j}) \times \\ \times (W_{cfhji}+W_{chfji}+W_{cjhfi}+W_{fchij}+W_{fchji})\,\, \\ - T^{h} \, (W_{bde}{}^{ij}+W_{bde}{}^{ji}+W_{bed}{}^{ji}+W_{dbe}{}^{ij}+W_{de}{}^{i}{}_{b}{}^{j}) \times \\ \times (W_{cfhij}+W_{chfij}+W_{cihfj}+W_{fchij}+W_{fchji}) \,=\, 0 \end{multline*} This result directly follows from the structure of summands and can be obtained by relabelling dummy indices and interchanging indices according to symmetries. Redberry simplifies this expression in approximately 2 milliseconds (right at parse) without any additional calculations. On the other hand, other systems need to expand out product of sums in order to determine that the result is zero; this, of course, is much more expensive calculation. In order to avoid additional expand operation, we generated sums (of size 100) of products of simple tensors with fixed number of free indices. So, the typical input problem looked as follows: \[ \require{color} \left( W{}^{\alpha\beta} \, T{}^{\nu}{}_{\beta\rho} \, R{}^{\theta\gamma\rho} \, F{}_{\mu\theta\alpha} \, + \, \dots \color{grey}\text{(99 terms)} \, \right) \,-\, \left( F{}_{\mu\rho\theta} \, W{}^{\theta\beta} \, R{}^{\rho\gamma\alpha} \, T{}^{\nu}{}_{\beta\alpha} \, +\, \dots \color{grey}\text{(99 terms)} \, \right) \, = \, 0 \]

The results of our are presented on Fig. 1 (all benchmarks were performed on the same hardware: AMD Phenom II X6 1100T; 16 Gb RAM; Ubuntu Linux 12.04). Left figure shows the dependence of time needed by system to obtain zero on the number of multipliers in products in target sum. In this benchmark we used a set of basic tensors with number of indices from 1 to 6 (e.g. $A_a$, $B_{ab}$, $C_{abc}$ etc.), number of “outer” free indices equal to 5 and varying number of product lengths from 4 to 18 (increasing this parameter, we thereby increased number of dummy indices).

We analysed both situation when simple tensors have symmetries (symmetric or antisymmetric with respect to all its indices) and not; unfortunately, in the first case Maple was unable to obtain zero on almost all used examples, so we excluded Maple in this case. In case without symmetries Redberry shows polynomial behaviour on number of multipliers, while Cadabra and xAct have small exponent and Maple has extremely large exponent or even factorial dependence (which shows that it uses some brute-force algorithm). In case with symmetries, all three systems (Cadabra, xAct and Redberry) have exponential dependence in the worst case, but Redberry has better behaviour on larger problems.

For the benchmark presented on the right picture in Fig. 1, we used sums of products with fixed length equal to 5, fixed number of “outer” free indices equal to 5 and with varying number of basic simple tensors with different number of indices (thereby affecting number of dummy indices) and measured time dependence on average number of indices in products. As in the first benchmark in the case without symmetries we observed polynomial dependence for Redberry, small exponent for xAct and Cadabra, and factorial in case of Maple. On the other hand, presence of symmetries almost does not change the behaviour of Cadabra and xAct, while Redberry failed to simplify large expressions in a reasonable time.

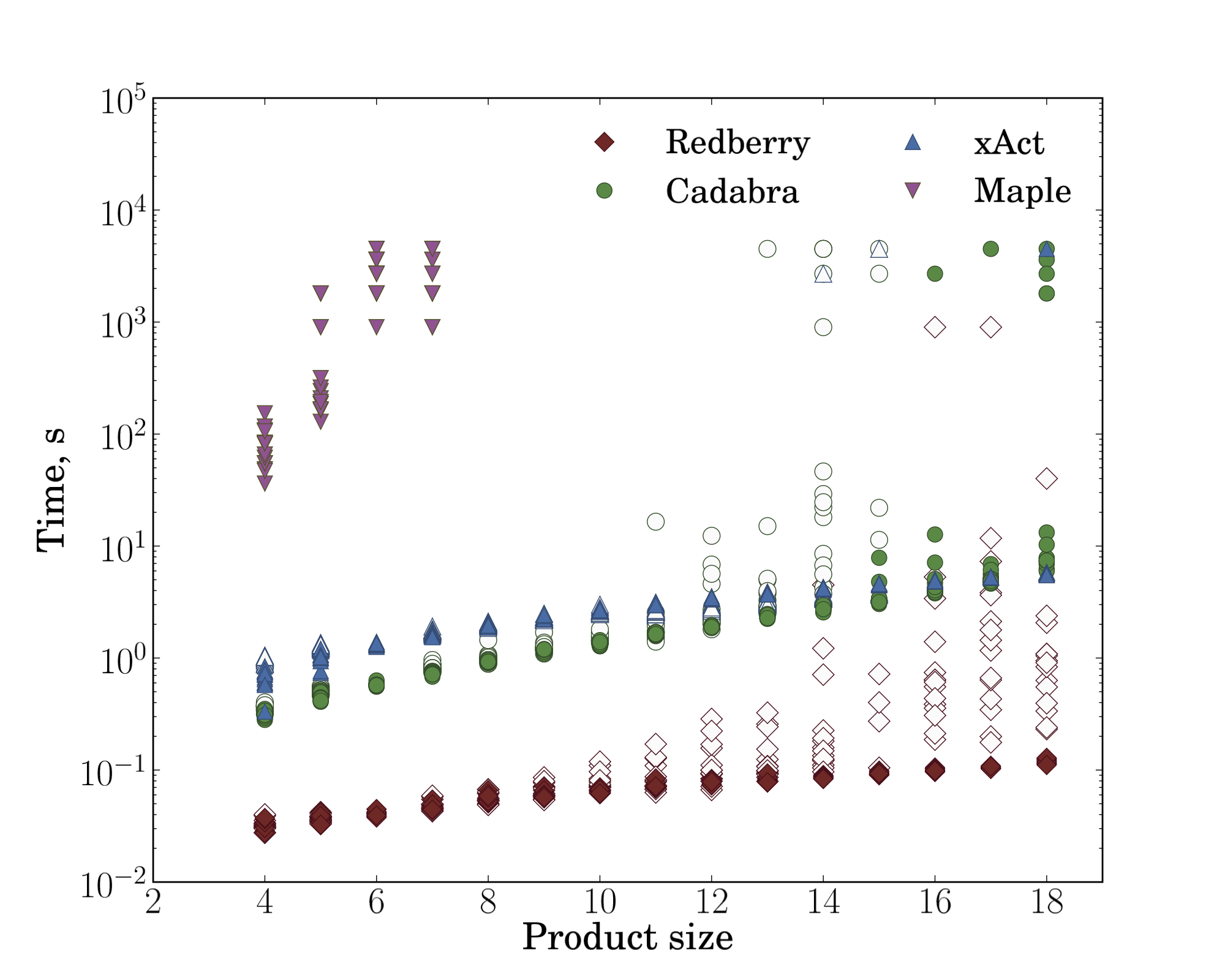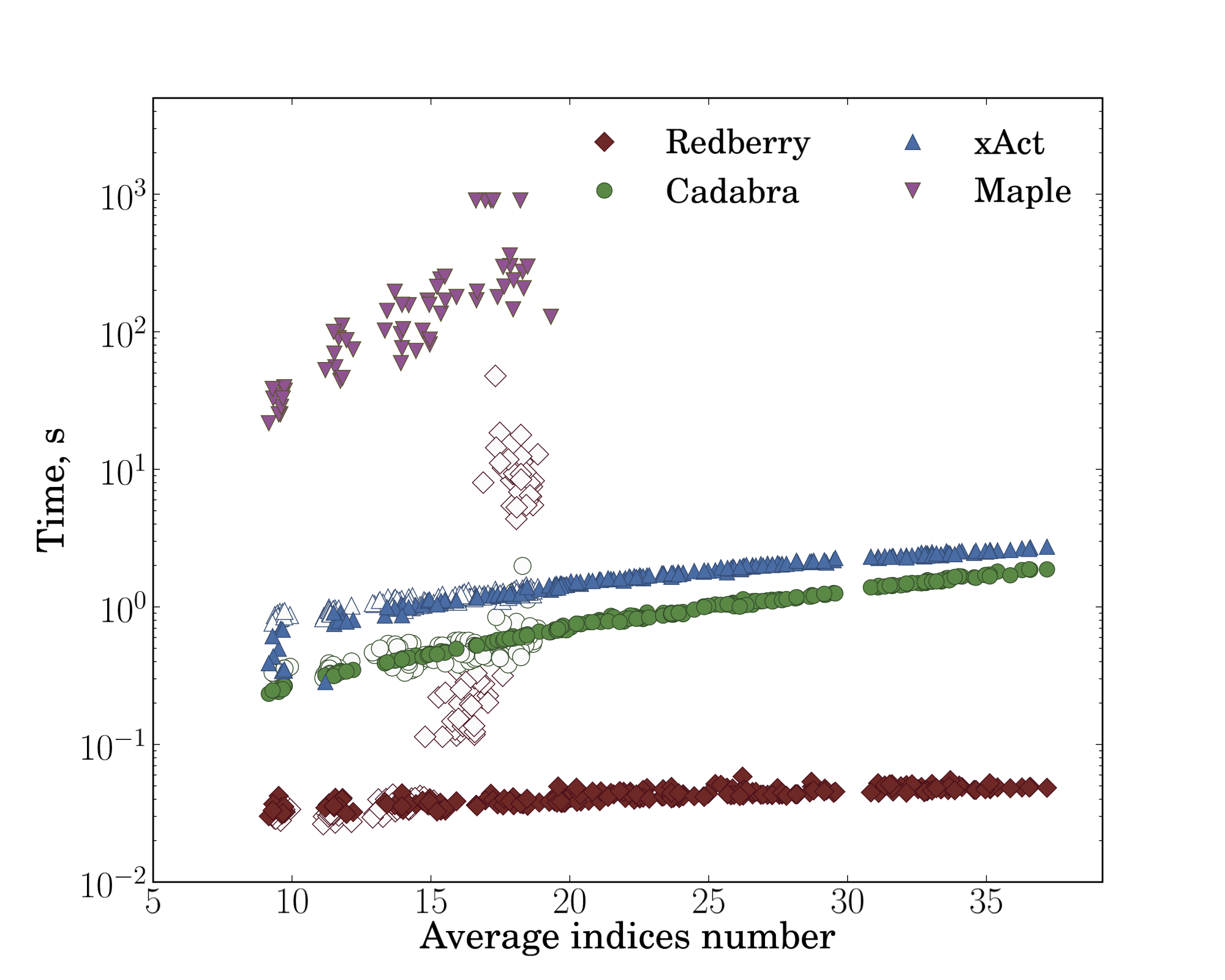Fig. 1: Dependence of time spent in simplification routine on product size (left) and on average number of indices in products (right). For these benchmarks we used sums (100 summands) of products of simple tensors, then subtracted it from itself (in equivalently rewritten form: shuffled summands and multipliers, renamed dummy indices and interchanged indices of simple tensors according to their symmetries) and measured time needed to obtain zero when simplifying inputs prepared in such a way. For Redberry, xAct and Cadabra we performed benchmarks both with (blank markers) and without symmetries (filled markers) of simple tensors, while Maple was unable to simplify such expressions in case with symmetries. The expressions used for these benchmarks can be found below.

Another important metric of CAS is its performance in simplification of expressions with deeply nested structure. For this benchmarks we generated sums of products of sums of products (so expression depth is 4) with following characteristics: we used basic tensors $A_a$, $B_{ab}$, $C_{abc}$, all generated expressions had one free index, varying product sizes from 2 to 4 and varying sum sizes from 2 to 4. So the used expressions looked like:

\begin{multline*} \left( F_{\mu\nu} \left( T^{\mu\alpha} R^{\nu\beta} \,+\, \dots \right) \,+\, \dots \right) \left( R_{\alpha\rho} \left( F^{\rho}{}_{\beta} R_{\tau\gamma}\phantom{{}^\beta} +\, \dots \right) \,+\, \dots \right) \,\times\, \left( \phantom{{}^\beta} \dots \phantom{{}^\beta} \right) \, \\ - \, \left( F_{\nu\mu}T^{\nu\beta}R^{\mu\alpha}R_{\beta\rho}F^{\rho}{}_{\alpha} R_{\tau\gamma} \,+\, \dots \right) \,=\, 0 \end{multline*}

Unfortunately, Maple Physics was unable to simplify any of provided examples (we've contacted with Maple Physics developers; they answered that it is unknown when functionality for simplification of these examples will be available), so we had to exclude Maple from consideration.

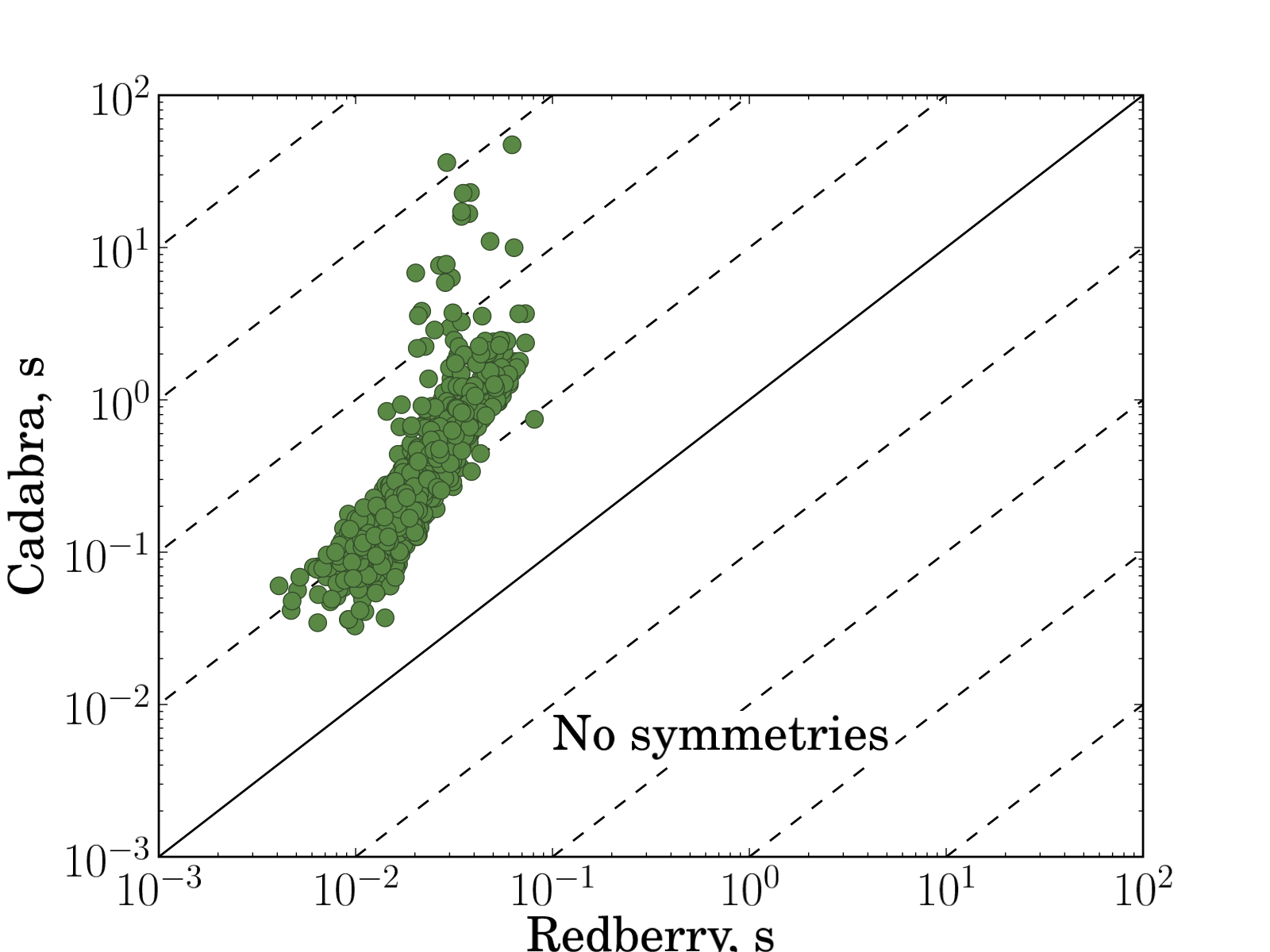
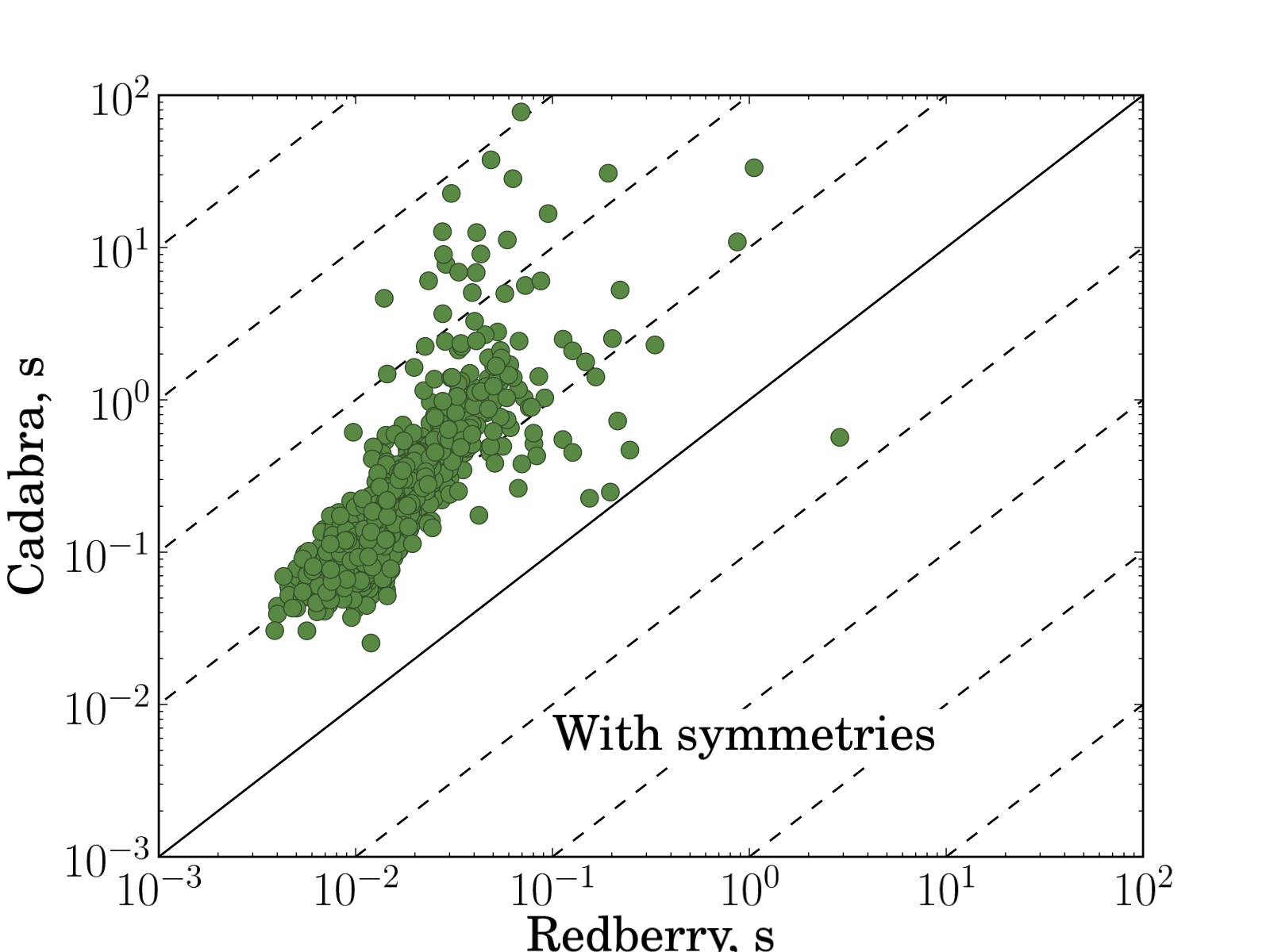
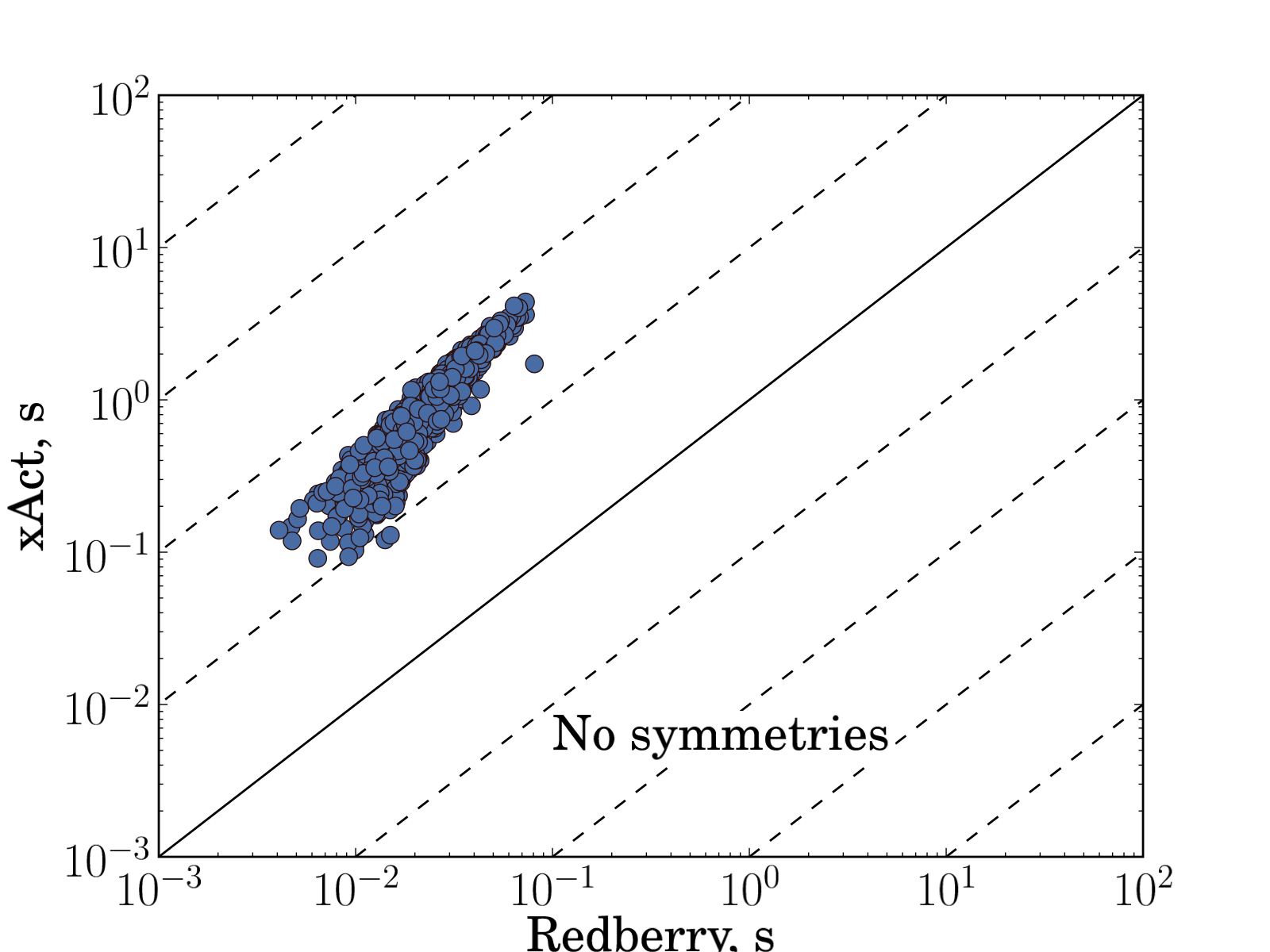
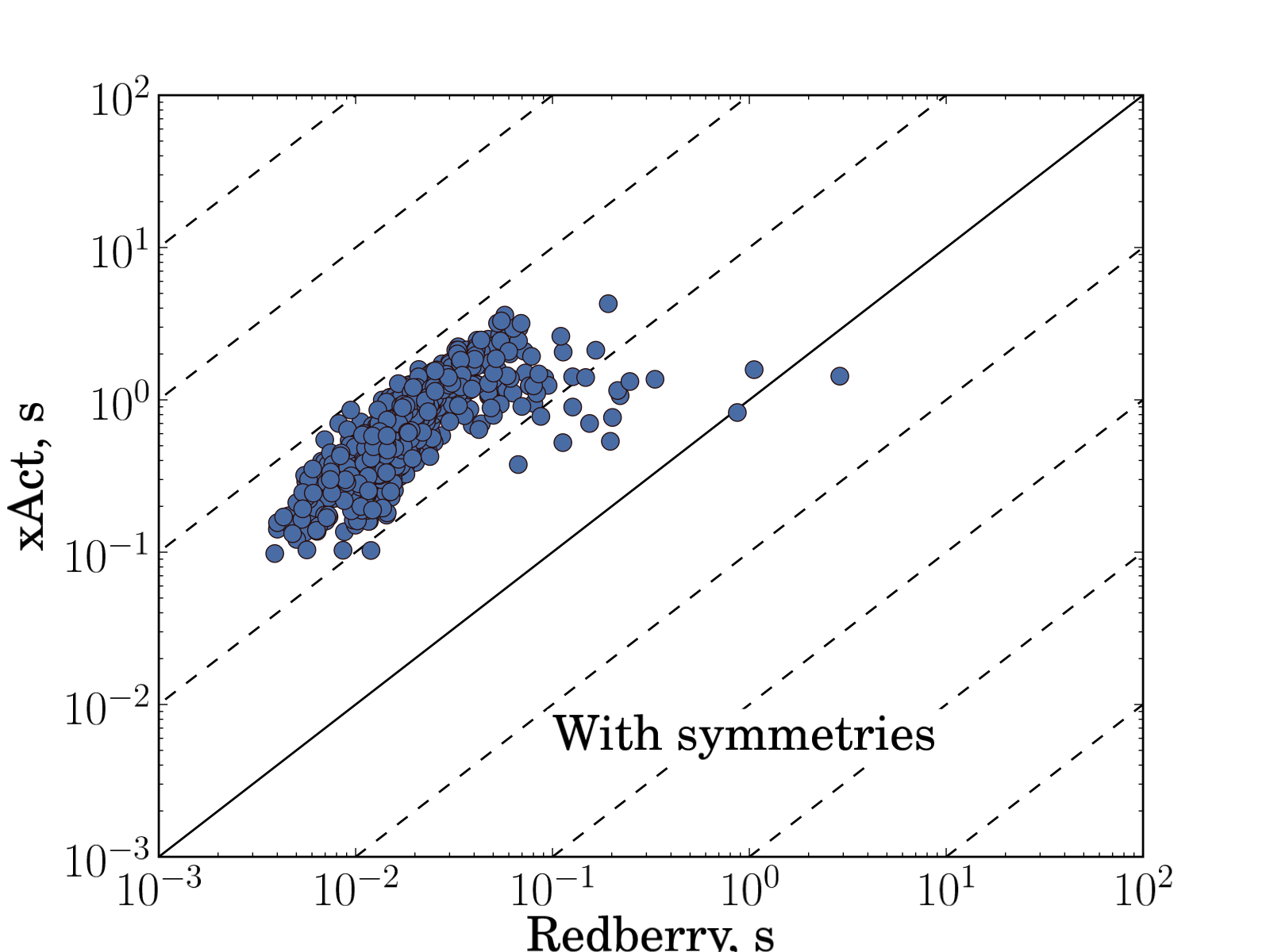
Fig. 2 shows the comparison of time spent in expand and collect operation for the same input expressions for Redberry vs. xAct, Redberry vs. Cadabra and xAct vs. Cadabra. We performed tests both in case when tensors have symmetries ($B_{ab}$ antisymmetric and $C_{abc}$ symmetric) and not. Summarizing all timings and taking the average, we found that Redberry is 41 times faster than xAct and 29 times faster than Cadabra in case without symmetries and 26 and 33 times faster in case with symmetries in our benchmarks. It is worth noting that such a performance gain can become much more significant in case of more complicated expressions, where size of intermediate expressions became larger, and in such cases Redberry can be even several thousands times faster because of its ability to simplify intermediate expressions during evaluation.

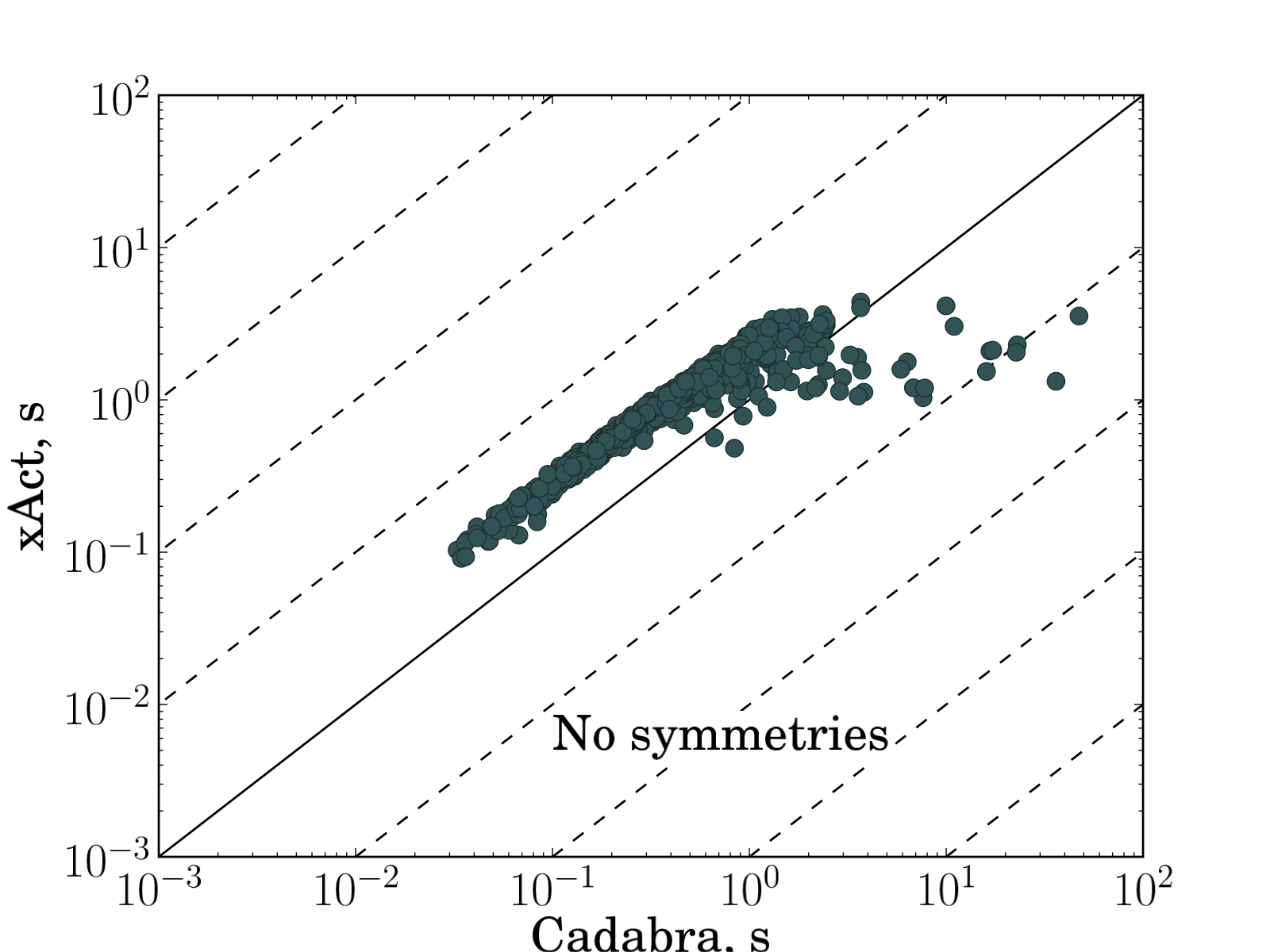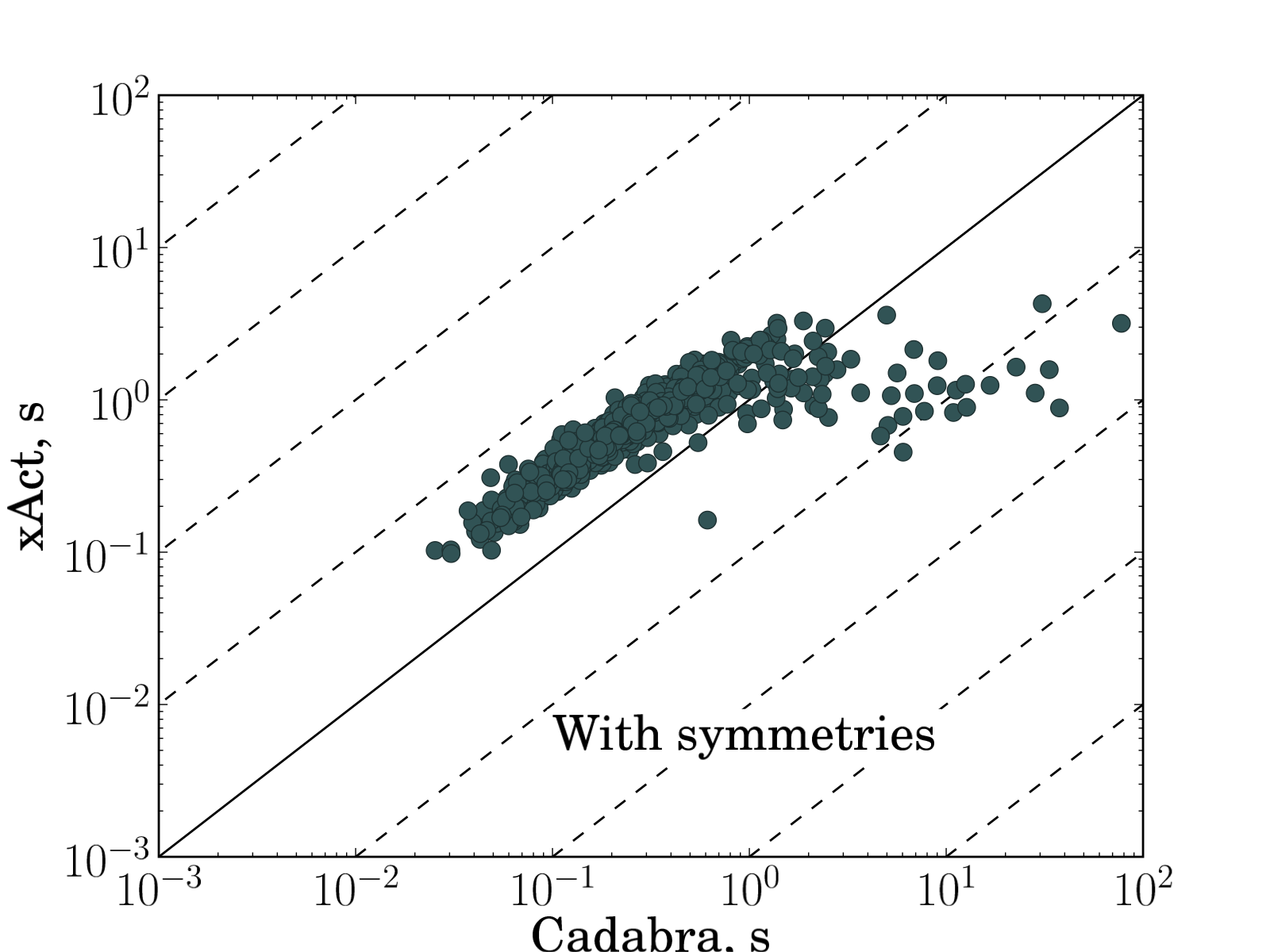Fig. 2: Comparison of time spent in simplification routine for randomly generated expressions. Each input problem plotted as filled circle. Each plot represents comparison of execution times needed to simplify input expression to zero between different systems (xAct versus Redberry, Cadabra versus Redberry, xAct versus Cadabra). Solid line corresponds to equal execution times, dashed lines shows 10x, 100x, 1000x, etc. execution time ratio. On average in presented benchmarks Redberry is 41 times faster than xAct and 29 times faster than Cadabra in case without symmetries and 26 and 33 times faster in case with symmetries. The expressions used for these benchmarks can be found below.

All expressions can be downloaded from:

http://bitbucket.org/redberry/benchmarking-expressions/src

The description of each file:

• expressions-product-size-no-sym.txt — Fig. 1 left without symmetries
• expressions-product-size-sym.txt — Fig. 1 left with symmetries
• expressions-indices-size-no-sym.txt — Fig. 1 right with no symmetries
• expressions-indices-size-sym.txt — Fig. 1 right with symmetries
• expressions-no-sym-rxc.txt — Fig. 2 without symmetries
• expressions-rxc.txt — Fig. 2 with symmetries

Each line in above files contains expression written in Redberry format. Lines with comments (starting with #) contains information about symmetries of used tensors.