Getting started

---

In order to install Redberry follow the instructions on the Installation page. The majority of code snippets presented on this site can be executed by wrapping them with the following Groovy code:

import cc.redberry.core.context.*
import cc.redberry.core.indices.*
import cc.redberry.core.tensor.*
import cc.redberry.core.transformations.*
import cc.redberry.groovy.Redberry

import static cc.redberry.core.tensor.Tensors.*
import static cc.redberry.core.indices.IndexType.*
import static cc.redberry.groovy.RedberryPhysics.*
import static cc.redberry.groovy.RedberryStatic.*
 
use(Redberry){
    //put your code here
}

However, some examples require additional import statements, in this case it will be specifically indicated in the description of the snippet.

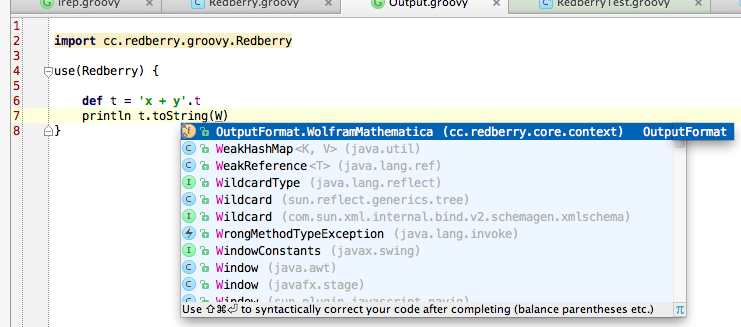
If you are using Redberry through IntelliJ IDEA (as recommended on the Installation page), work with code will be sufficiently simplified by many useful features of the IDE like code completion, syntax highlighting and automatic importing. Just start typing some Redberry statement (or press additionally Ctrl + Space or Ctrl + Space + Space) and IntelliJ will automatically suggest a correct function name and insert import statement if necessary:

When you are using Redberry, you are actually coding in a Groovy language, so the main language features are inherited from Groovy. Besides, Redberry provides a lot of special syntax constructions that make a general Groovy syntax more convenient for the purposes of computer algebra.

Two basic things that one need to know before starting any calculations with Redberry are how to define expressions and how to apply transformations to them (substitutions, simplifications etc.). Let's start from a preliminary overview of how these things can be done in Redberry via Groovy syntax.

To input expression by hand and bind it to a variable one can do:

 
def expr = 'a * F^{A}_{B \\mu \\nu}'.t
println expr

  > a * F^{A}_{B \\mu \\nu}

Here '…'.t syntax is used to convert a string representation of expression into a computer object. The input notation for tensors is nearly identical to $\LaTeX{}$ syntax for mathematical expressions with minor syntax modifications. Some additional constraints on expressions arise form Einstein notation.

Transformations can be applied by right shift >> operator in the following way:

 
def expr = '(x + y) * a'.t
println Expand >> expr

   > x * a + y * a

Here Expand is a Transformation (for the list of all available transformations see List of common transformations). In order to apply several transformations sequentially one can use join operator &:

 
def t = '(g_mn + h_mn) * (h^mn - g^nm)'.t
t = (Expand & EliminateMetrics) >> t
println t

   > -d^{n}_{n} + h^{mn} * h_{mn}

One can find more information about transformations on Applying and manipulating transformations page.

From the last example one can also see that Redberry uses a predefined notation for metric tensor g_{mn} and for Kronecker delta d^m_n. Since in the majority of cases the dimension of the space affects only trace of Kronecker tensor (d^n_n), Redberry does not bind a particular dimension to each index type (thus one can use different dimensions for different index types).

One can define and apply substitution in Redberry in the following way:

def subs = 'f_mn = t_mn + k_mn'.t
def tensor = 'f_ab * (f^ab + f^ba)'.t
println subs >> tensor

   > (t_ab + k_ab) * (t^ab + t^ba + k^ab + k^ba)

For further reading about substitutions in Redberry see Substitutions page.

Let's consider a minimal real physical example in order to quickly dive into Redberry. The example demonstrates calculation of differential cross section of the Compton scattering in scalar massless Quantum Electrodynamics (QED) (the reader which is not familiar with this area can skip physical details and focus just on the algebraic operations):

// photon-scalar-scalar vertex
def V1 = 'V_i[p_a, q_b] = -I*e*(p_i+q_i)'.t
// photon-photon-scalar-scalar vertex
def V2 = 'V_{ij} = 2*I*e**2*g_{ij}'.t
// scalar propagator for massless particle
def P = 'D[k_a] = -I/(k^a*k_a)'.t
// matrix element
def M = ('M^ij ='
        + 'V^i[k3_a,k3_a+k1_a]*D[k3_a+k1_a]*V^j[-k4_a,-k3_a-k1_a]'
        + '+V^j[k3_a,k3_a-k2_a]*D[k3_a-k2_a]*V^i[-k3_a+k2_a,-k4_a]'
        + '+V^ij').t
// substituting vertices and propagator in matrix element
M = (V1 & V2 & P) >> M
// squared matrix element
// minus here is due to complex conjugation
def M2 = M >> 'M2 = -M_ij*M^ij'.t
// expand squared matrix element and
// eliminate metrics and Kronecker deltas
M2 = (ExpandAll & EliminateMetrics) >> M2
M2 = 'd_i^i = 4'.t >> M2 //substitute dimension 4

// massless particles
// k1_a*k1^a = 0, k2_a*k2^a = 0 etc.
for (def i in 1..4)
    M2 = "k${i}_a*k${i}^a = 0".t >> M2

// momentum conservation
M2 = ('k1_a*k2^a = k3_a*k4^a'.t
        & 'k1_a*k3^a = k2_a*k4^a'.t
        & 'k1_a*k4^a = k2_a*k3^a'.t) >> M2

// factor terms
M2 = Factor >> M2
println M2

This script will print a well-known expression for the squared matrix element of the Compton scattering in massless scalar QED: \begin{equation*} |\mathcal{M}|^2 = -\frac{e^{4}}{2} \frac{-18 (k_2 k_3) (k_2 k_4)+(k_3 k_4)^{2}+(k_2 k_3)^{2}+2( (k_2 k_3)- (k_2 k_4)) (k_3 k_4)+(k_2 k_4)^{2}}{(k_2 k_3)(k_2 k_4)}, \end{equation*} where $(k\,p)$ denotes scalar product $k_i p^i$.

This example reproduces a typical basic steps needed to solve almost any problem: we define expressions, apply substitutions and other simplifications in order to obtain the result. The code above speaks for itself, so leaving aside the physical aspects of the problem, let's focus only on a few programming aspects.

In the first few lines we defined substitutions that will be applied to matrix element defined in line 8. Functions (tensorial functions that depend on a list of arguments) in Redberry can be defined using square brackets. So, line 2

def V1 = 'V_i[p_a, q_b] = -I*e*(p_i+q_i)'.t

defines a function of two tensorial arguments (built-in symbol I stands for the imaginary unit): $$V_{i}(p_i, q_b) = -i e (p_i+q_i) $$ When applying such substitution to an expression, the arguments of function are matched automatically:

def V1 = 'V_i[p_a, q_b] = -I*e*(p_i+q_i)'.t
println V1 >> 'V_a[k_i +p_i, p_i]*V^a[k_i-p_i,k_i]'.t

   > -e**2*(2*k^{a}-p^{a})*(k_{a}+2*p_{a})

All transformations in Redberry (e.g. substitutions, Expand, EliminateMetrics etc.) are first-class objects and can be assigned to a variable. They can be applied to mathematical expression using >> operator. Detailed discussion on Redberry transformations usage and list of basic built-in transformations can be found on Applying and manipulating transformations and List of common transformations pages.

The last point that should be discussed here is looping construct used in lines 24, 25. Here standard Groovy syntax is used to apply several similar substitutions ($k_{1i} k_1{}^i = 0$, $k_{2i} k_2{}^i = 0$ and so on). So, the code

for (def i in 1..4)
    M2 = "k${i}_a*k${i}^a = 0".t >> M2

is a shorthand for

M2 = "k1_a*k1^a = 0".t >> M2
M2 = "k2_a*k2^a = 0".t >> M2
M2 = "k3_a*k3^a = 0".t >> M2
M2 = "k4_a*k4^a = 0".t >> M2

• Related guides: Inputting and printing mathematical expressions, Applying and manipulating transformations, List of common transformations