Table of Contents

Compton scattering in scalar QED

Theory

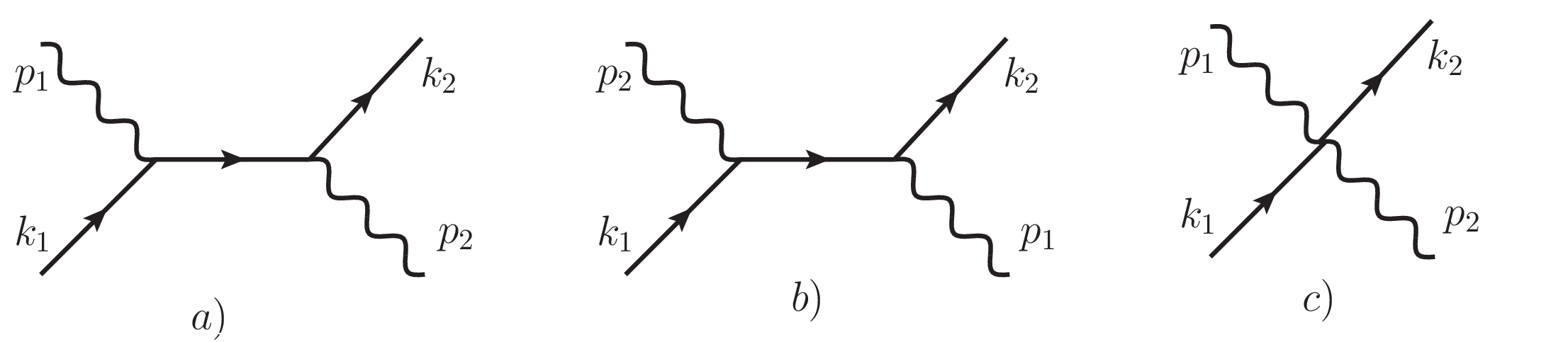
Let us consider Compton scattering in scalar QED. There are three Feynman diagrams:

The Feynman rules for scalar QED are: \begin{eqnarray} \mbox{scalar propagator:}&\qquad& D(k) = \frac{-i}{k^2 - m^2}, \\ \mbox{photon-scalar-scalar vertex:} &\qquad& V_\mu(k, p) = -i\, e\, (k_\mu + p_\mu), \\ \mbox{photon-photon-scalar-scalar vertex:} &\qquad& V_{\mu\nu} = 2 \, i \, e^2 \, g_{\mu\nu}, \end{eqnarray} where $e$ is a scalar charge and in the second formula $k$ is incoming and $p$ outcoming scalar field momentum.

Using these Feynman rules it is easy to write amplitudes corresponding to the above Feynman diagrams:

\begin{eqnarray} \mbox{diagram a):}&\qquad& (\mathcal M_a)_{\mu\nu} = V_\mu(k_1, k_1 + p_1) \, D(k_1 + p_1) V_\nu(-k_2, -k_1 - p_1),\\ \mbox{diagram b):}&\qquad& (\mathcal M_b)_{\mu\nu} = V_\nu(k_1, k_1 - p_2) \, D(k_1 - p_2) V_\mu(-k_2, -k_1 + p_2),\\ \mbox{diagram c):}&\qquad& (\mathcal M_c)_{\mu\nu} = V_{\mu\nu}, \end{eqnarray} where $\mu$ and $\nu$ are indices of incoming and outcoming photon momentums. Total matrix element is \[ \mathcal M_{\mu\nu} = (\mathcal M_a)_{\mu\nu} \,+\, (\mathcal M_b)_{\mu\nu} \,+\, (\mathcal M_c)_{\mu\nu} \]

The final goal is squared matrix element summed over final and averaged over initial photon polsrizations:

\[ \frac{1}{2}\sum |\mathcal M|^2 = \frac{1}{2} \, \mathcal M^*_{\mu\nu} \mathcal M^{\mu\nu} \]

Code

The following Redberry code reproduces the typical steps needed to obtain the result: 

//photon-scalar-scalar vertex
def V1 = 'V_i[p_a, q_b] = -I*e*(p_i+q_i)'.t
//photon-photon-scalar-scalar vertex
def V2 = 'V_{ij} = 2*I*e**2*g_{ij}'.t
//scalar propagator
def P = 'D[k_a] = -I/(k^a*k_a - m**2)'.t
//diagram a)
def Ma = 'V^i[k1_a,k1_a+p1_a]*D[k1_a+p1_a]*V^j[-k2_a,-k1_a-p1_a]'.t
//diagram b)
def Mb = 'V^j[k1_a,k1_a-p2_a]*D[k1_a-p2_a]*V^i[-k2_a,-k1_a+p2_a]'.t
//diagram c)
def Mc = 'V^ij'.t
//total matrix element
def M = "M^ij = ${Ma + Mb + Mc}".t
//substituting vertices and propagator in matrix element
M = (V1 & V2 & P) >> M
//squared matrix element
//here minus is due to complex conjugation
def M2 = M >> 'M2 = M_ij*M^ij/2'.t
//define mandelstam and mass shell substitutions
def mandelstam = setMandelstam(
        [p1_a: '0', k1_a: 'm', p2_a: '0', k2_a: 'm'])
//expand squared matrix element and
//eliminate metrics and Kronecker deltas
M2 = (ExpandAll & EliminateMetrics & mandelstam) >> M2
//set space-time dimension
M2 = 'd_i^i = 4'.t >> M2
//simplify the result
M2 = ('u = 2*m**2-s-t'.t & Factor) >> M2
println M2

   > M2 = -4*(-4*m**2*s**3+6*m**4*s**2+m**4*t**2+s**2*t**2
          +2*s*m**4*t+2*s**3*t+m**8+s**4-4*s*m**6-4*m**2*s**2*t
          )*e**4*(-s+m**2-t)**(-2)*(s-m**2)**(-2)
This code will print the well known result: \begin{multline*} \frac{1}{2}\sum |\mathcal M|^2 = - \frac{4\, e^4}{(s-m^{2})^2\,(-s-t+m^{2})^2}\,\left(m^8 - 4m^6s + 6m^4s^2 -4m^2s^3 +\right.\\ \left.+ s^4 + 2m^4st - 4m^2s^2t + 2s^3t + m^4t^2 + s^2t^2\right), \end{multline*}

See also