Compton scattering in QED

Theory

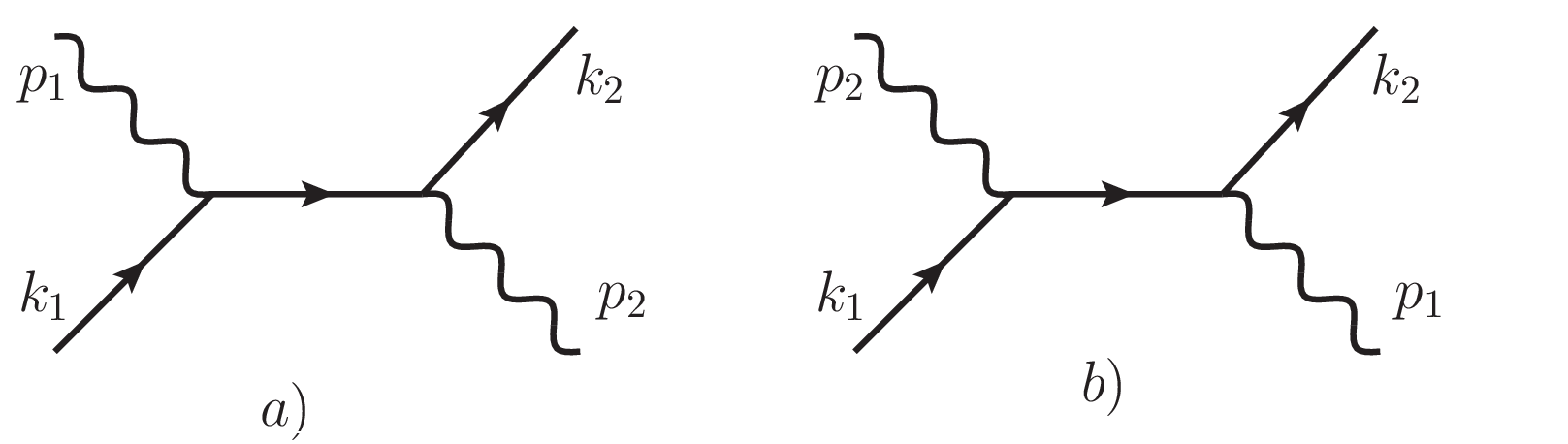
Let us consider Compton scattering in spinor QED. There are two Feynman diagrams:

The Feynman rules for spinor QED are: \begin{eqnarray} \mbox{electron propagator:}&\qquad& D(k) = \frac{-i\,\left(m + k_\mu \gamma^\mu \right)}{m^2 - k^2}, \\ \mbox{photon-electron-electron vertex:} &\qquad& V_\mu = -i\, e\, \gamma_ \mu, \end{eqnarray} where $e$ is an electron charge and $\gamma_\mu$ is Dirac matrix.

Using these Feynman rules it is easy to write amplitudes corresponding to the above Feynman diagrams:

\begin{eqnarray} \mbox{diagram a):}&\qquad& \mathcal M_a =\bar u(k_2)\, V_\mu \, \epsilon^\mu (p_2) \, D(k_1 + p_1) \, V_\nu \, \epsilon^\nu (p_1) \, u(k_1), \\ \mbox{diagram b):}&\qquad& \mathcal M_b =\bar u(k_2)\, V_\mu \, \epsilon^\mu (p_1) \, D(k_1 - p_2) \, V_\nu \, \epsilon^\nu (p_2) \, u(k_1), \end{eqnarray} where $u$ and $\bar u$ are electron wave function and its conjugation respectively and $\epsilon$ is a polarisation vector of photon.

The final goal is squared matrix element summed over final and averaged over initial polarisations:

\[ \frac{1}{4}\sum |\mathcal M|^2 = \frac{1}{4} \, \sum \, (\mathcal M_a + \mathcal M_b)^* (\mathcal M_a + \mathcal M_b) \]

Sum over photon and electron polarizations: \begin{gather} \sum\, \epsilon_\mu(p)\, \epsilon_\nu(p) \,=\, - g_{\mu\nu}\\ \sum\, u(k) \, \bar u(k)\, = \,m\, +\, k^\mu\,\gamma_\mu \end{gather}

The final standard thing is complex conjugation of matrix element. This can be done using the following obvious formula: \[ \left( \bar u(p_2)\, \gamma_{\alpha_1} \,\gamma_{\alpha_2}\,\dots \gamma_{\alpha_n} \, u(p_1) \right)^* = \bar u(p_1)\, \gamma_{\alpha_n} \,\gamma_{\alpha_{n-1}}\,\dots \gamma_{\alpha_1} \, u(p_2) \]

After summing squared matrix element over polarisations, all combinations of gamma matrices will automatically transform to combinations of gamma matrices traces.

Code

The following code reproduces exactly same steps as one need to perform with paper and pencil to calculate squared matrix element of Compton scattering: 

//setting up matrices
//gamma, vertex, propagator
defineMatrices 'G_a', 'V_i', 'D[x_m]', Matrix1.matrix,
        //electron wave function
        'vu[p_a]', Matrix1.vector,
        //its conjugation
        'cu[p_a]', Matrix1.covector
//vertex
def V = 'V_m = -I*e*G_m'.t
//electron propagator
def D = 'D[p_m] = -I*(m + p_m*G^m)/(m**2 - p_m*p^m)'.t
//diagram a)
def Ma = 'cu[k2_m]*V_m*e^m[p2_m]*D[k1_m+p1_m]*V_n*e^n[p1_m]*vu[k1_m]'.t
//diagram b)
def Mb = 'cu[k2_m]*V_m*e^m[p1_m]*D[k1_m-p2_m]*V_n*e^n[p2_m]*vu[k1_m]'.t
//total matrix element
def M = Ma + Mb
//substituting Feynman rules
M = (V & D) >> M
//list of Mandelstam and mass shell substitutions
def mandelstam = setMandelstam(
        [p1_a: '0', k1_a: 'm', p2_a: '0', k2_a: 'm'])
//simplify matrix element
M = (ExpandAll & EliminateMetrics & mandelstam) >> M
//conjugate matrix element
def MC = 'vu[k1_m]*cu[k2_m] = vu[k2_m]*cu[k1_m]'.t >> M
MC = (Conjugate & Reverse[Matrix1]) >> MC
//squared matrix element
def M2 = ExpandAll >> (M * MC / 4)
//sum over photon polarizations
M2 = 'e_m[p1_a]*e_n[p1_a] = -g_mn'.t >> M2
M2 = 'e_m[p2_a]*e_n[p2_a] = -g_mn'.t >> M2
//sum over electron polarizations
M2 = 'vu[k2_m]*cu[k2_m] = m + k2^m*G_m'.t >> M2
M2 = 'vu[k1_m]*cu[k1_m] = m + k1^m*G_m'.t >> M2
//taking trace of gamma matrices
M2 = DiracTrace['G_a'] >> M2
//simplify the result
M2 = (ExpandAndEliminate & mandelstam) >> M2
//substitute space-time dimension
M2 = 'd^i_i = 4'.t >> M2
//final simplifications
M2 = 'u = 2*m**2 -s-t'.t >> M2
M2 = Factor >> M2
println M2

   > 2*e**4*(2*m**8-t**3*m**2+t**3*s-8*s**2*t*m**2+3*t**2*m**4+4*t*m**4*s
         +4*s**3*t-2*t**2*m**2*s+2*s**4+3*s**2*t**2-8*s**3*m**2+12*s**2*m**4
         -8*m**6*s)*(-t+m**2-s)**(-2)*(-m**2+s)**(-2)
This code will print well known Klein-Nishina-Tamm formula: \begin{multline*} \frac{1}{4} \sum \,|\mathcal M|^2 \,=\, \frac{2\,e^4 }{(m^{2}-s)^2 (-m^{2}+s+t)^2} \, \times \\ \times \, \left( -8 s^{2} m^{2} t+4 s^{3} t+2 s^{4}+t^{3} s+2 m^{8}+4 m^{4} s t-m^{2} t^{3} \right. \\ \left.-2 m^{2} t^{2} s+3 m^{4} t^{2}-8 s^{3} m^{2}+12 s^{2} m^{4}+3 s^{2} t^{2}-8 m^{6} s \right) \end{multline*}

See also